
🐟 Acoustic Receiver Array Design and Movement Simulation
Optimizing Telemetry Systems and Simulating Fish Movement Patterns
Jake Brownscombe
2025-09-16
Source:vignettes/Array_Design_Simulation.Rmd
Array_Design_Simulation.RmdAnalysis Overview
This tutorial demonstrates acoustic telemetry array design and movement simulation using the positionR package. This workflow provides tools for optimizing receiver placement, modeling detection efficiency, and simulating realistic fish movement patterns to evaluate system performance.
Key Applications: - 📡 Optimize receiver array configurations for maximum coverage - 📊 Generate detection efficiency models based on distance and depth - 🐟 Simulate realistic fish movements and generate detection patterns - 🏡 Estimate space use and home range from simulated data - 🌿 Analyze habitat selection patterns
Ideal for researchers planning acoustic telemetry studies who want to evaluate different array designs and predict system performance before field deployment. These tools are also useful in conjuction with positioning algorithms to determine optimal settings (see WADE tutorial).
🚀 Setup & Data Preparation
Load Environmental Data
We’ll use the example depth raster of Stoney Lake, Ontario, Canada included in the package:
# Load example depth raster
data("depth_raster")
raster::crs(depth_raster) <- "EPSG:32617" # UTM Zone 17N
# View raster properties
depth_raster## class : RasterLayer
## dimensions : 127, 168, 21336 (nrow, ncol, ncell)
## resolution : 100, 100 (x, y)
## extent : 720304, 737104, 4929241, 4941941 (xmin, xmax, ymin, ymax)
## crs : +proj=utm +zone=17 +datum=WGS84 +units=m +no_defs
## source : memory
## names : layer
## values : -32.49542, 0 (min, max)
# Quick visualization
plot(depth_raster, main = "Study Area: Stoney Lake, Ontario",
col = colorRampPalette(c("darkblue", "lightblue"))(50))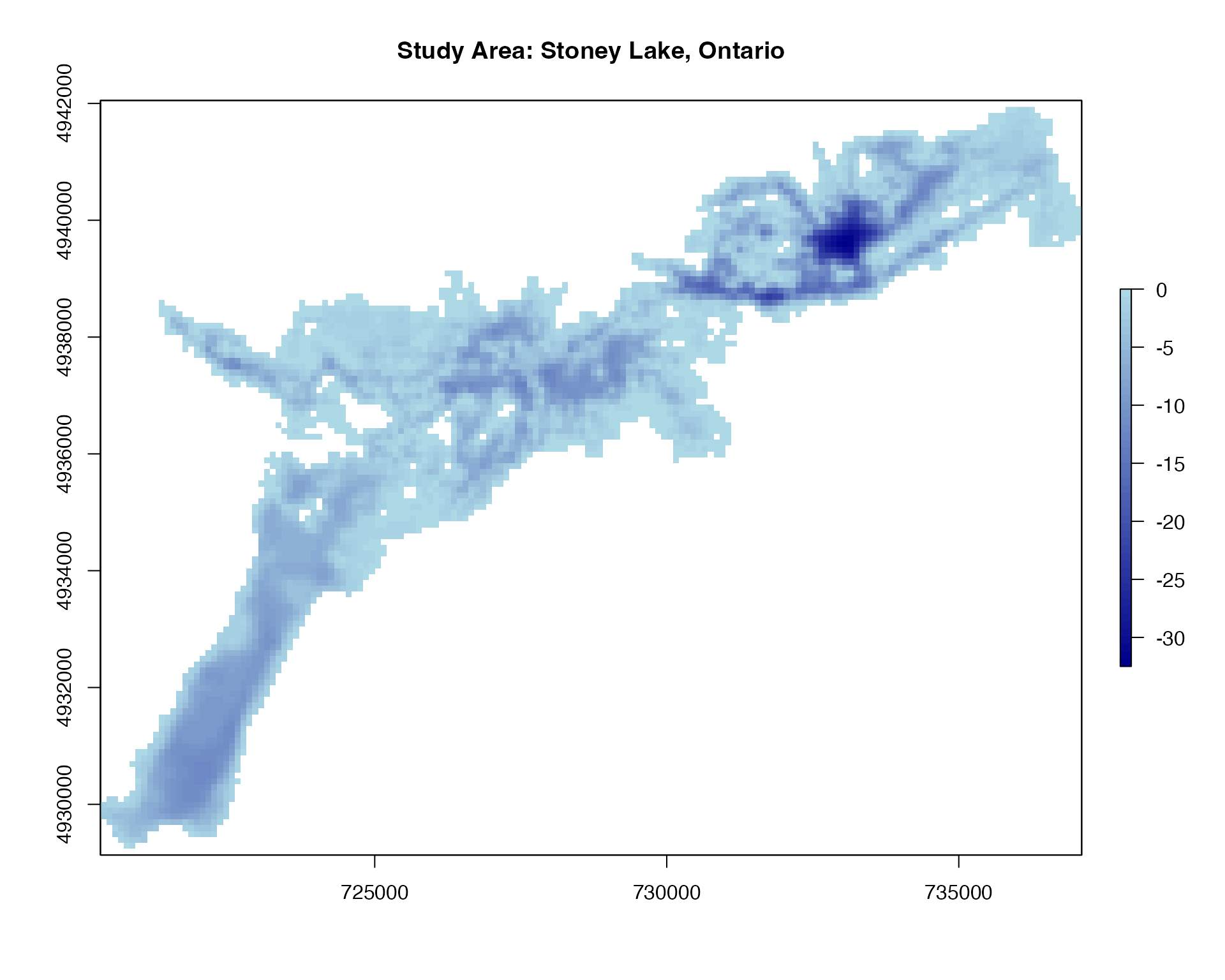
📡 Receiver Array Design
The first critical step in acoustic telemetry is designing an effective receiver array. The spatial configuration of receivers determines detection coverage, positioning accuracy, and ultimately the quality of movement/space use data collected.
Generate Array Configurations
positionR provides three methods for generating receiver stations with different spatial arrangements:
# Regular spacing - specified number of points in systematic pattern
stations_regular <- generate_regular_points(depth_raster, n_points = 100, seed = 123)
# Fixed spacing - points separated by specified distance
stations_spaced <- generate_spaced_points(depth_raster, spacing = 1000, seed = 123)
# Random locations - randomly distributed points
stations_random <- generate_random_points(depth_raster, n_points = 100, seed = 123)
# View station data structure
stations_spaced # Note: includes depth values for each station## Simple feature collection with 44 features and 4 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 720804 ymin: 4929741 xmax: 735804 ymax: 4940741
## Projected CRS: WGS 84 / UTM zone 17N
## First 10 features:
## geometry x y station_id raster_value
## 1 POINT (720804 4929741) 720804 4929741 1 -4.4574073
## 2 POINT (721804 4929741) 721804 4929741 2 -4.2318250
## 3 POINT (721804 4930741) 721804 4930741 3 -11.3425511
## 4 POINT (721804 4931741) 721804 4931741 4 -6.6432655
## 5 POINT (722804 4931741) 722804 4931741 5 -5.2543719
## 6 POINT (722804 4932741) 722804 4932741 6 -5.7718487
## 7 POINT (722804 4933741) 722804 4933741 7 -1.2150741
## 8 POINT (723804 4933741) 723804 4933741 8 -3.6121938
## 9 POINT (723804 4934741) 723804 4934741 9 -2.5111908
## 10 POINT (724804 4934741) 724804 4934741 10 -0.6993271
# Visualize different array configurations
plot_points_on_input(depth_raster, stations_regular) 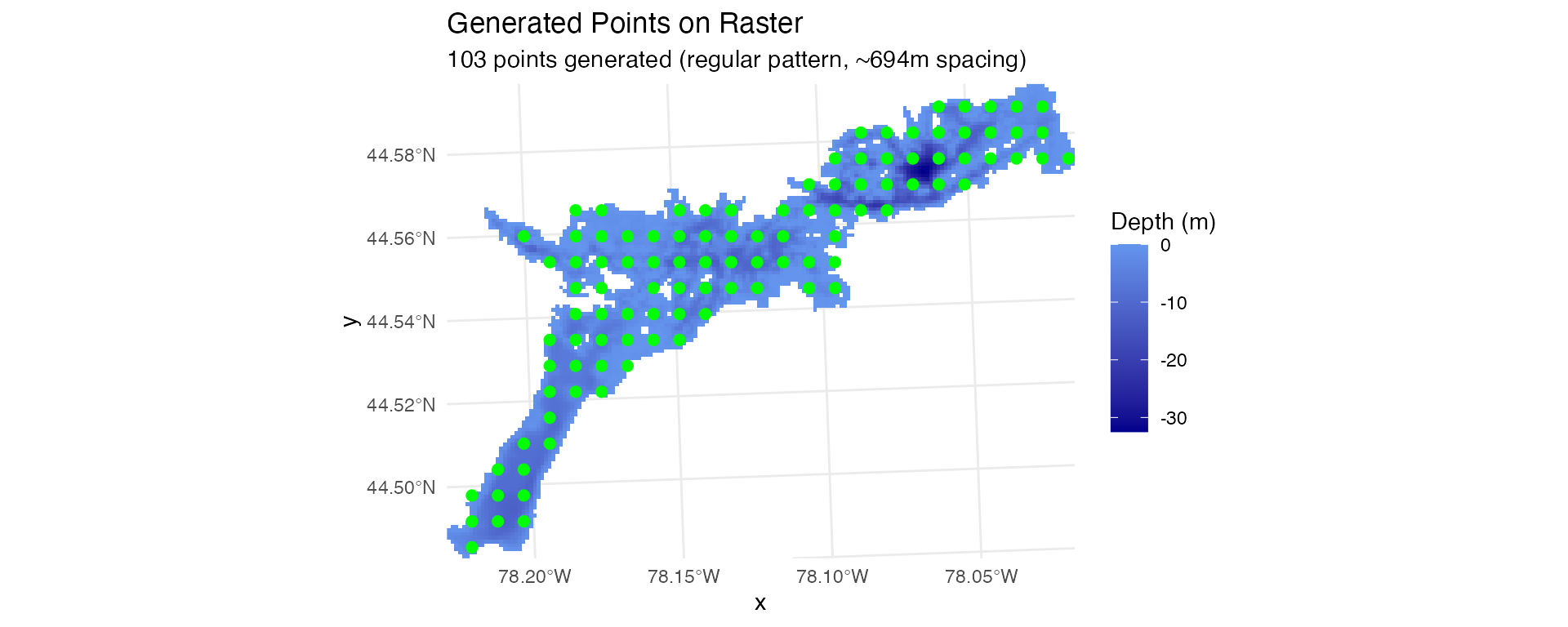
plot_points_on_input(depth_raster, stations_spaced) 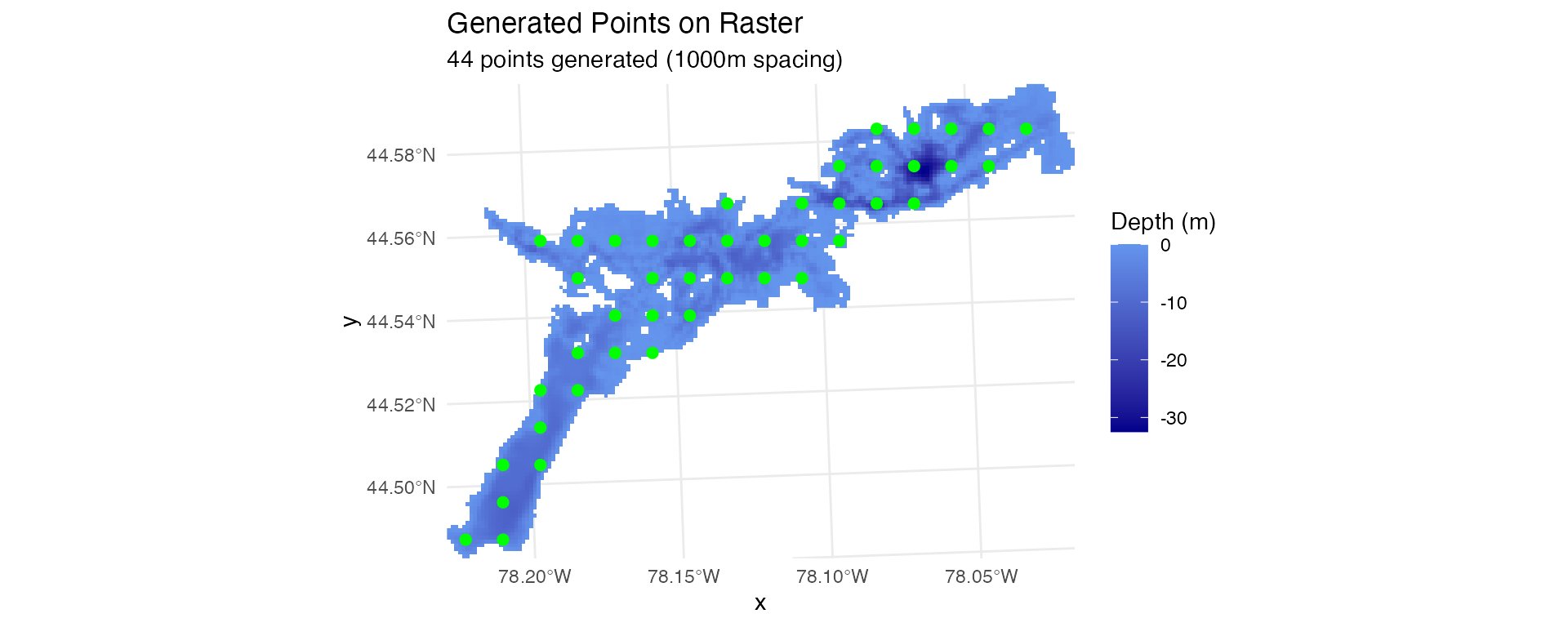
plot_points_on_input(depth_raster, stations_random) 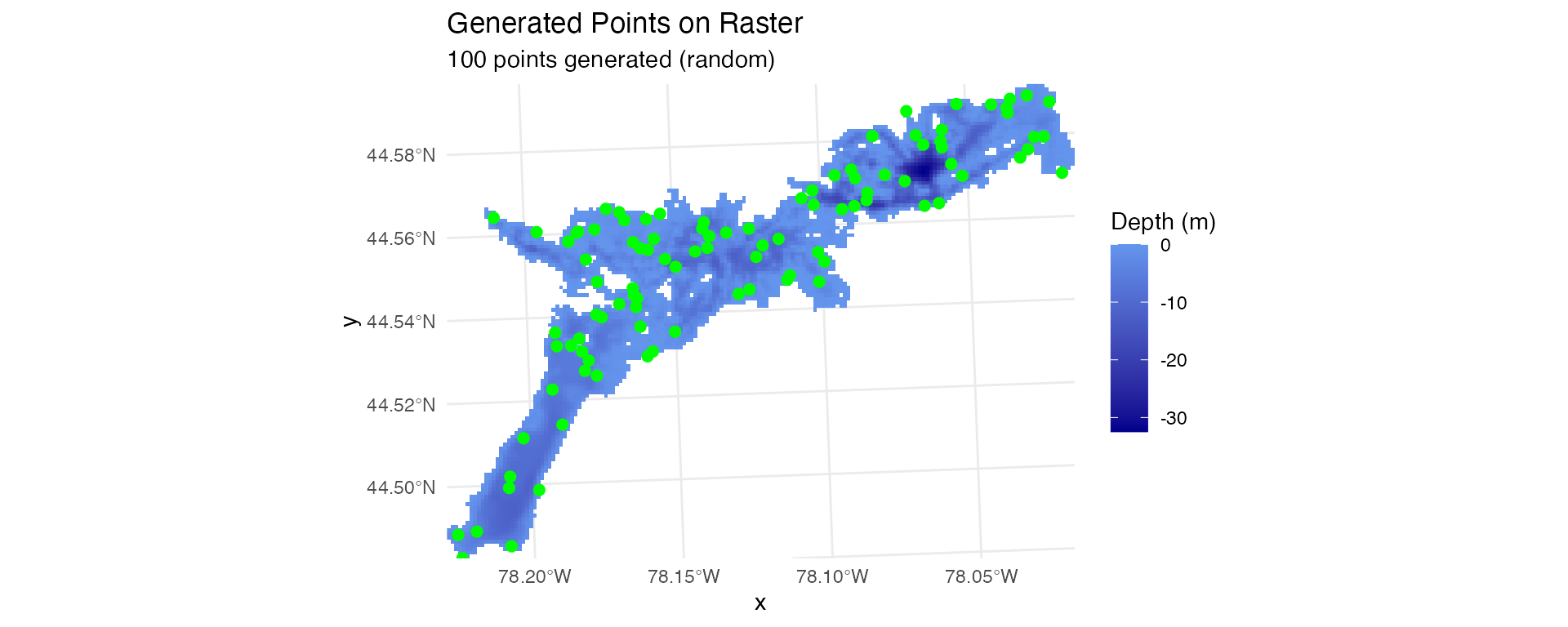
Calculate Station Distances
Calculate cost-distance and straight-line distance from each receiver to all raster cells. This is essential for modeling detection efficiency across the study area:
# Calculate shortest path distances, straight line distances, and tortuosity
station_distances <- calculate_station_distances(
raster = depth_raster,
receiver_frame = stations_regular,
station_col = "station_id",
max_distance = 30000 # 30 km maximum distance
)## Creating transition matrix...
## Calculating distances for station 1 of 103 (ID: 1 )
## Calculating distances for station 2 of 103 (ID: 2 )
## Calculating distances for station 3 of 103 (ID: 3 )
## Calculating distances for station 4 of 103 (ID: 4 )
## Calculating distances for station 5 of 103 (ID: 5 )
## Calculating distances for station 6 of 103 (ID: 6 )
## Calculating distances for station 7 of 103 (ID: 7 )
## Calculating distances for station 8 of 103 (ID: 8 )
## Calculating distances for station 9 of 103 (ID: 9 )
## Calculating distances for station 10 of 103 (ID: 10 )
## Calculating distances for station 11 of 103 (ID: 11 )
## Calculating distances for station 12 of 103 (ID: 12 )
## Calculating distances for station 13 of 103 (ID: 13 )
## Calculating distances for station 14 of 103 (ID: 14 )
## Calculating distances for station 15 of 103 (ID: 15 )
## Calculating distances for station 16 of 103 (ID: 16 )
## Calculating distances for station 17 of 103 (ID: 17 )
## Calculating distances for station 18 of 103 (ID: 18 )
## Calculating distances for station 19 of 103 (ID: 19 )
## Calculating distances for station 20 of 103 (ID: 20 )
## Calculating distances for station 21 of 103 (ID: 21 )
## Calculating distances for station 22 of 103 (ID: 22 )
## Calculating distances for station 23 of 103 (ID: 23 )
## Calculating distances for station 24 of 103 (ID: 24 )
## Calculating distances for station 25 of 103 (ID: 25 )
## Calculating distances for station 26 of 103 (ID: 26 )
## Calculating distances for station 27 of 103 (ID: 27 )
## Calculating distances for station 28 of 103 (ID: 28 )
## Calculating distances for station 29 of 103 (ID: 29 )
## Calculating distances for station 30 of 103 (ID: 30 )
## Calculating distances for station 31 of 103 (ID: 31 )
## Calculating distances for station 32 of 103 (ID: 32 )
## Calculating distances for station 33 of 103 (ID: 33 )
## Calculating distances for station 34 of 103 (ID: 34 )
## Calculating distances for station 35 of 103 (ID: 35 )
## Calculating distances for station 36 of 103 (ID: 36 )
## Calculating distances for station 37 of 103 (ID: 37 )
## Calculating distances for station 38 of 103 (ID: 38 )
## Calculating distances for station 39 of 103 (ID: 39 )
## Calculating distances for station 40 of 103 (ID: 40 )
## Calculating distances for station 41 of 103 (ID: 41 )
## Calculating distances for station 42 of 103 (ID: 42 )
## Calculating distances for station 43 of 103 (ID: 43 )
## Calculating distances for station 44 of 103 (ID: 44 )
## Calculating distances for station 45 of 103 (ID: 45 )
## Calculating distances for station 46 of 103 (ID: 46 )
## Calculating distances for station 47 of 103 (ID: 47 )
## Calculating distances for station 48 of 103 (ID: 48 )
## Calculating distances for station 49 of 103 (ID: 49 )
## Calculating distances for station 50 of 103 (ID: 50 )
## Calculating distances for station 51 of 103 (ID: 51 )
## Calculating distances for station 52 of 103 (ID: 52 )
## Calculating distances for station 53 of 103 (ID: 53 )
## Calculating distances for station 54 of 103 (ID: 54 )
## Calculating distances for station 55 of 103 (ID: 55 )
## Calculating distances for station 56 of 103 (ID: 56 )
## Calculating distances for station 57 of 103 (ID: 57 )
## Calculating distances for station 58 of 103 (ID: 58 )
## Calculating distances for station 59 of 103 (ID: 59 )
## Calculating distances for station 60 of 103 (ID: 60 )
## Calculating distances for station 61 of 103 (ID: 61 )
## Calculating distances for station 62 of 103 (ID: 62 )
## Calculating distances for station 63 of 103 (ID: 63 )
## Calculating distances for station 64 of 103 (ID: 64 )
## Calculating distances for station 65 of 103 (ID: 65 )
## Calculating distances for station 66 of 103 (ID: 66 )
## Calculating distances for station 67 of 103 (ID: 67 )
## Calculating distances for station 68 of 103 (ID: 68 )
## Calculating distances for station 69 of 103 (ID: 69 )
## Calculating distances for station 70 of 103 (ID: 70 )
## Calculating distances for station 71 of 103 (ID: 71 )
## Calculating distances for station 72 of 103 (ID: 72 )
## Calculating distances for station 73 of 103 (ID: 73 )
## Calculating distances for station 74 of 103 (ID: 74 )
## Calculating distances for station 75 of 103 (ID: 75 )
## Calculating distances for station 76 of 103 (ID: 76 )
## Calculating distances for station 77 of 103 (ID: 77 )
## Calculating distances for station 78 of 103 (ID: 78 )
## Calculating distances for station 79 of 103 (ID: 79 )
## Calculating distances for station 80 of 103 (ID: 80 )
## Calculating distances for station 81 of 103 (ID: 81 )
## Calculating distances for station 82 of 103 (ID: 82 )
## Calculating distances for station 83 of 103 (ID: 83 )
## Calculating distances for station 84 of 103 (ID: 84 )
## Calculating distances for station 85 of 103 (ID: 85 )
## Calculating distances for station 86 of 103 (ID: 86 )
## Calculating distances for station 87 of 103 (ID: 87 )
## Calculating distances for station 88 of 103 (ID: 88 )
## Calculating distances for station 89 of 103 (ID: 89 )
## Calculating distances for station 90 of 103 (ID: 90 )
## Calculating distances for station 91 of 103 (ID: 91 )
## Calculating distances for station 92 of 103 (ID: 92 )
## Calculating distances for station 93 of 103 (ID: 93 )
## Calculating distances for station 94 of 103 (ID: 94 )
## Calculating distances for station 95 of 103 (ID: 95 )
## Calculating distances for station 96 of 103 (ID: 96 )
## Calculating distances for station 97 of 103 (ID: 97 )
## Calculating distances for station 98 of 103 (ID: 98 )
## Calculating distances for station 99 of 103 (ID: 99 )
## Calculating distances for station 100 of 103 (ID: 100 )
## Calculating distances for station 101 of 103 (ID: 101 )
## Calculating distances for station 102 of 103 (ID: 102 )
## Calculating distances for station 103 of 103 (ID: 103 )
## Converting to long format...
## Distance calculations complete!
## Result contains 496254 station-cell combinations
## Station IDs ( integer ): 1, 2, 3, 4, 5 ...
# Visualize distance field for one receiver
ggplot(station_distances %>% filter(station_no == 1),
aes(x, y, fill = cost_distance)) +
geom_raster() +
scale_fill_viridis_c(option = "magma", name = "Distance (m)") +
geom_point(data = stations_regular %>% filter(station_id == 1),
aes(x, y), col = "green", size = 4, inherit.aes = FALSE) +
labs(title = "Cost Distance Field from Station 1",
subtitle = "Green point = station location") +
theme_minimal() +
coord_sf()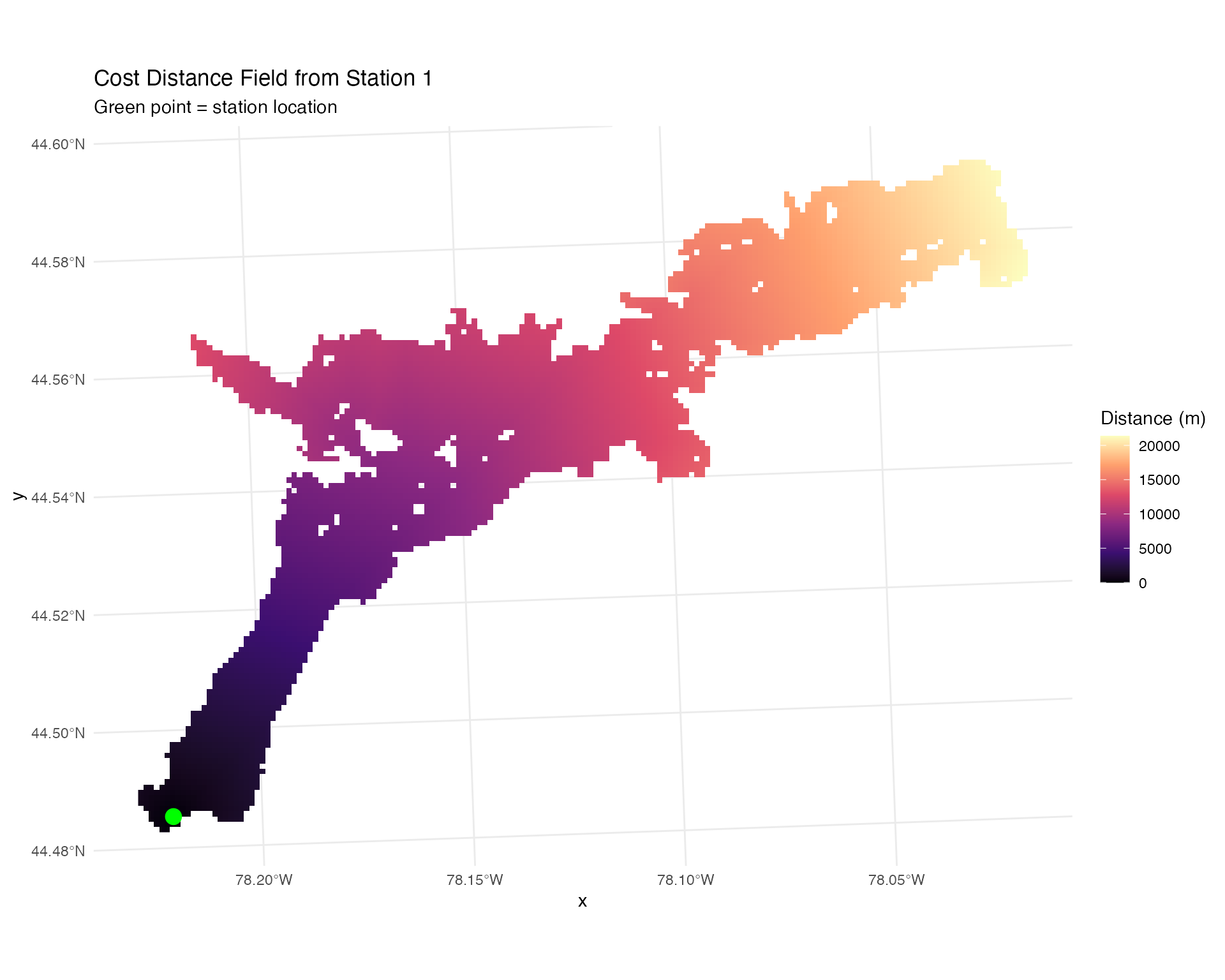
ggplot(station_distances %>% filter(station_no == 1),
aes(x, y, fill = tortuosity)) +
geom_raster() +
scale_fill_viridis_c(option = "magma", name = "Tortuosity", limits=c(0.9,1.5)) +
geom_point(data = stations_regular %>% filter(station_id == 1),
aes(x, y), col = "green", size = 4, inherit.aes = FALSE) +
labs(title = "Tortuosity Field from Station 1",
subtitle = "Green point = station location") +
theme_minimal() +
coord_sf()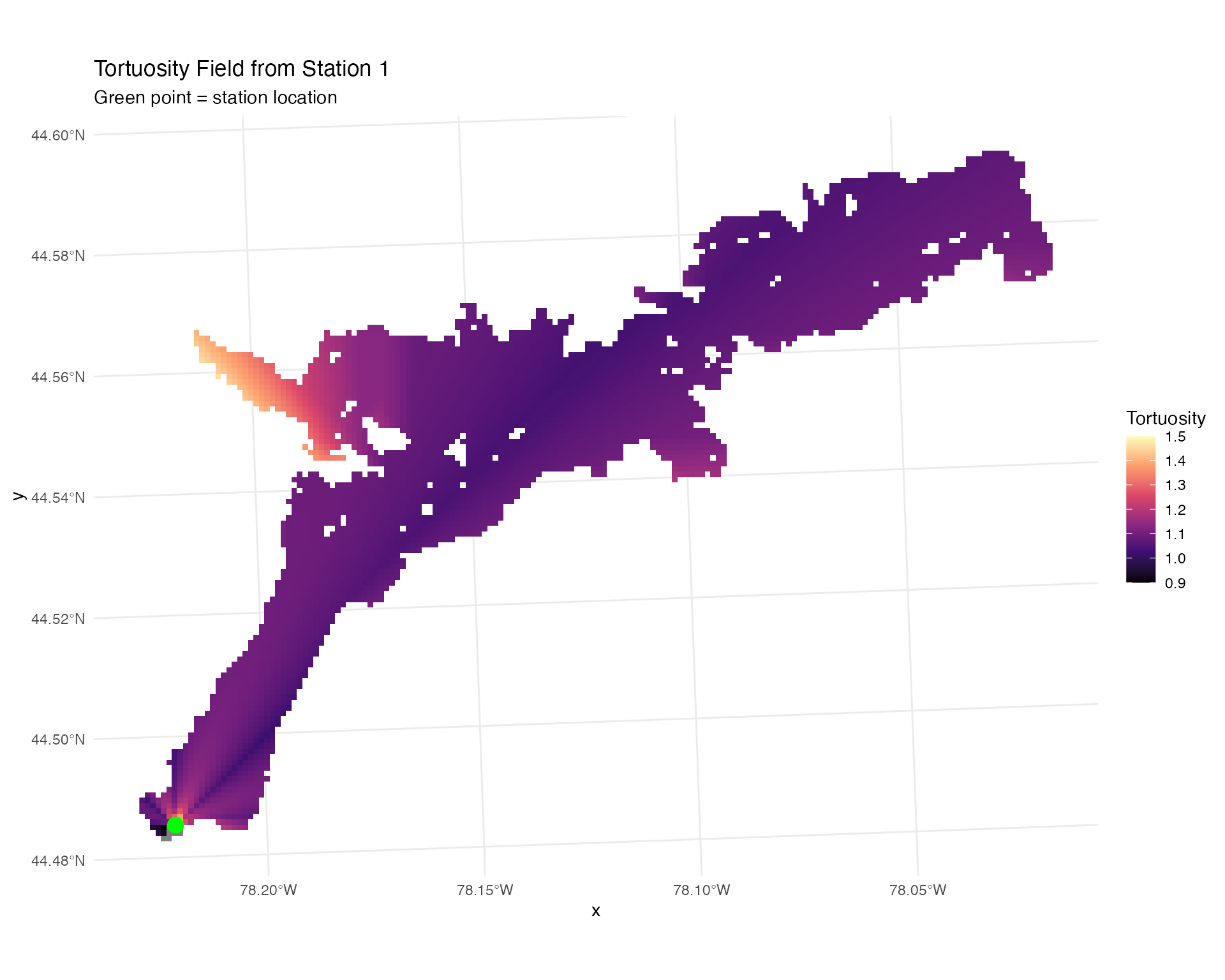
📊 Detection Range Modeling
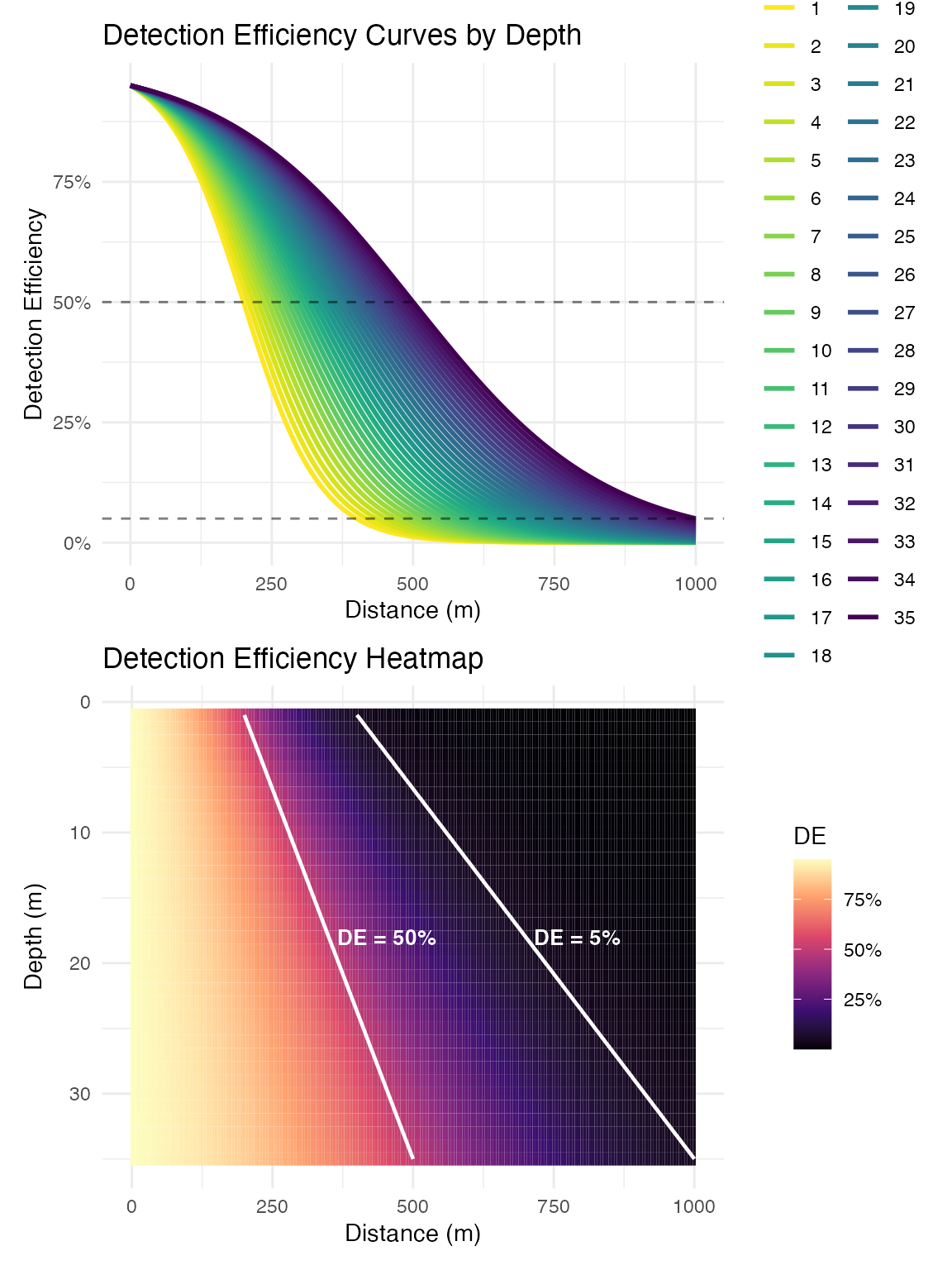
Detection range is highly variable and depends on environmental conditions, e.g. depth, temperature, substrate type, and ambient noise. Accurate detection models are essential for understanding system performance and interpreting detection patterns. This function can be used to generate basic detection range curves, although it is recommended to collect and model system specific conditions for application.
Create Depth-Dependent Detection Model
Model detection efficiency as a function of distance and depth. This example is reasonably representative of inland lake conditions, but is not dynamic over time:
# Create logistic detection efficiency model
# These parameters should be based on empirical range testing
logistic_DE <- create_logistic_curve_depth(
min_depth = 1, # Minimum depth (m)
max_depth = 35, # Maximum depth (m)
d50_min_depth = 200, # 50% detection range at min depth (m)
d95_min_depth = 400, # 5% detection range at min depth (m)
d50_max_depth = 500, # 50% detection range at max depth (m)
d95_max_depth = 1000, # 5% detection range at max depth (m)
plot = TRUE,
return_model = TRUE,
return_object = TRUE
)
##
## Call:
## stats::glm(formula = DE ~ dist_m * depth_m, family = stats::binomial(link = "logit"),
## data = predictions)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.256280 -0.034500 0.008532 0.043991 0.087721
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.612e+00 1.653e-01 15.803 <2e-16 ***
## dist_m -1.180e-02 4.809e-04 -24.547 <2e-16 ***
## depth_m 1.554e-02 7.635e-03 2.035 0.0418 *
## dist_m:depth_m 1.715e-04 1.897e-05 9.041 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 4232.395 on 7034 degrees of freedom
## Residual deviance: 25.731 on 7031 degrees of freedom
## AIC: 2666.2
##
## Number of Fisher Scoring iterations: 7
# The fitted model can be used for predictions
summary(logistic_DE$log_model)##
## Call:
## stats::glm(formula = DE ~ dist_m * depth_m, family = stats::binomial(link = "logit"),
## data = predictions)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.256280 -0.034500 0.008532 0.043991 0.087721
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.612e+00 1.653e-01 15.803 <2e-16 ***
## dist_m -1.180e-02 4.809e-04 -24.547 <2e-16 ***
## depth_m 1.554e-02 7.635e-03 2.035 0.0418 *
## dist_m:depth_m 1.715e-04 1.897e-05 9.041 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 4232.395 on 7034 degrees of freedom
## Residual deviance: 25.731 on 7031 degrees of freedom
## AIC: 2666.2
##
## Number of Fisher Scoring iterations: 7Apply Detection Model
Apply the detection range model to predict detection efficiency for each receiver across the study area:
# Predict detection efficiency for each receiver-cell combination
station_distances$DE_pred <- stats::predict(
logistic_DE$log_model,
newdata = station_distances %>%
rename(dist_m = cost_distance) %>%
mutate(depth_m = abs(raster_value)),
type = "response"
)
# Visualize detection efficiency field for one station
ggplot(station_distances %>% filter(station_no == 10),
aes(x, y, fill = DE_pred)) +
geom_raster() +
scale_fill_viridis_c(option = "magma", name = "Detection\nEfficiency") +
labs(title = "Detection Efficiency Field - Station 10",
subtitle = "Probability of detecting a transmission") +
theme_minimal() +
coord_sf()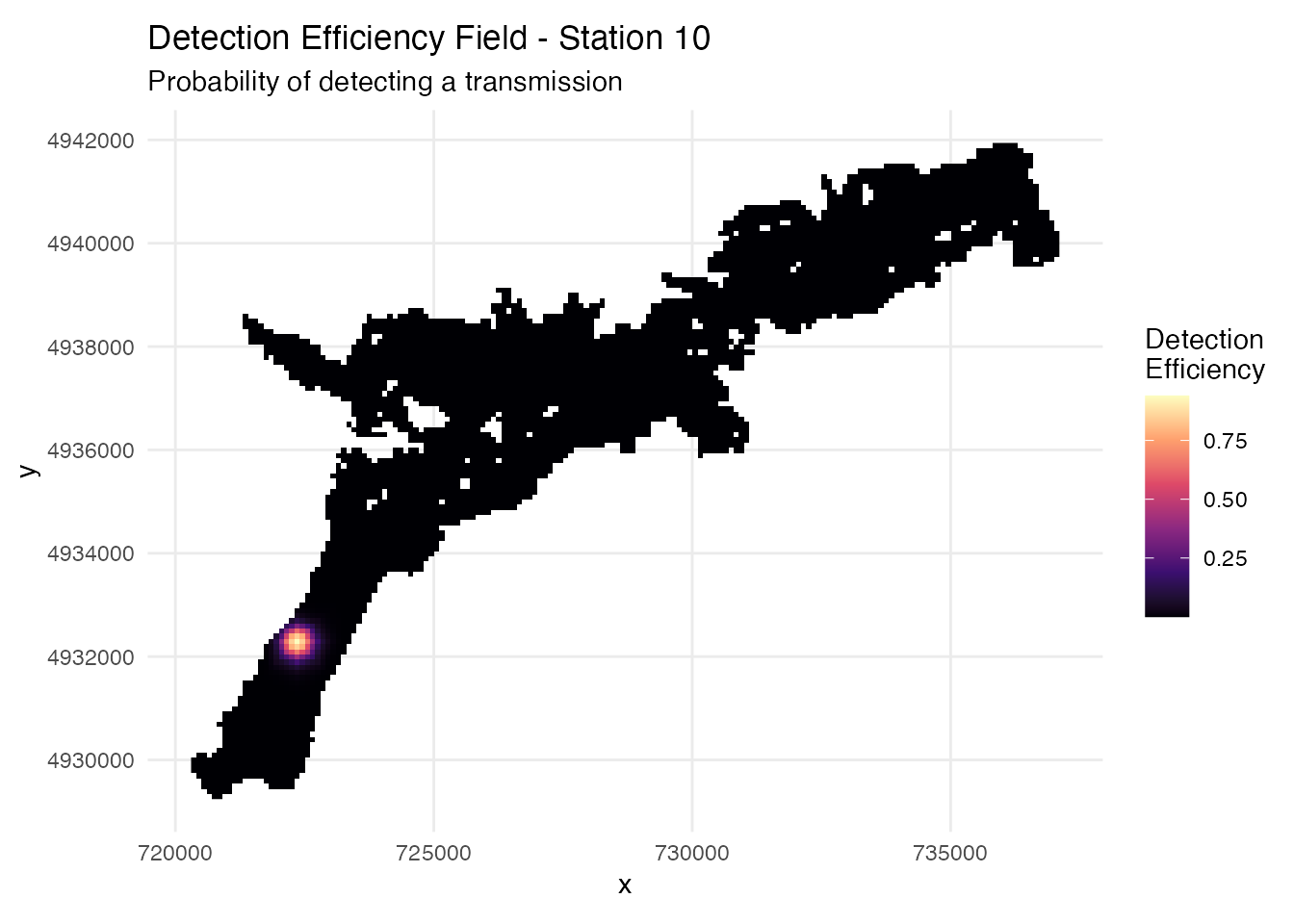
System-Wide Detection Coverage
Analyze detection performance at the system level to evaluate array design effectiveness:
# Calculate system-level detection probabilities
# Options: "cumulative" (any receiver), "3_plus" (≥3 receivers), "both"
system_DE <- calculate_detection_system(
distance_frame = station_distances,
receiver_frame = stations_regular,
model = logistic_DE$log_model,
output_type = "cumulative", # Fast computation
plots = TRUE
)## Using all 103 stations (no date filtering)
## Calculating detection probabilities...
## Using existing DE_pred column
## Calculating system probabilities...
## Creating plots...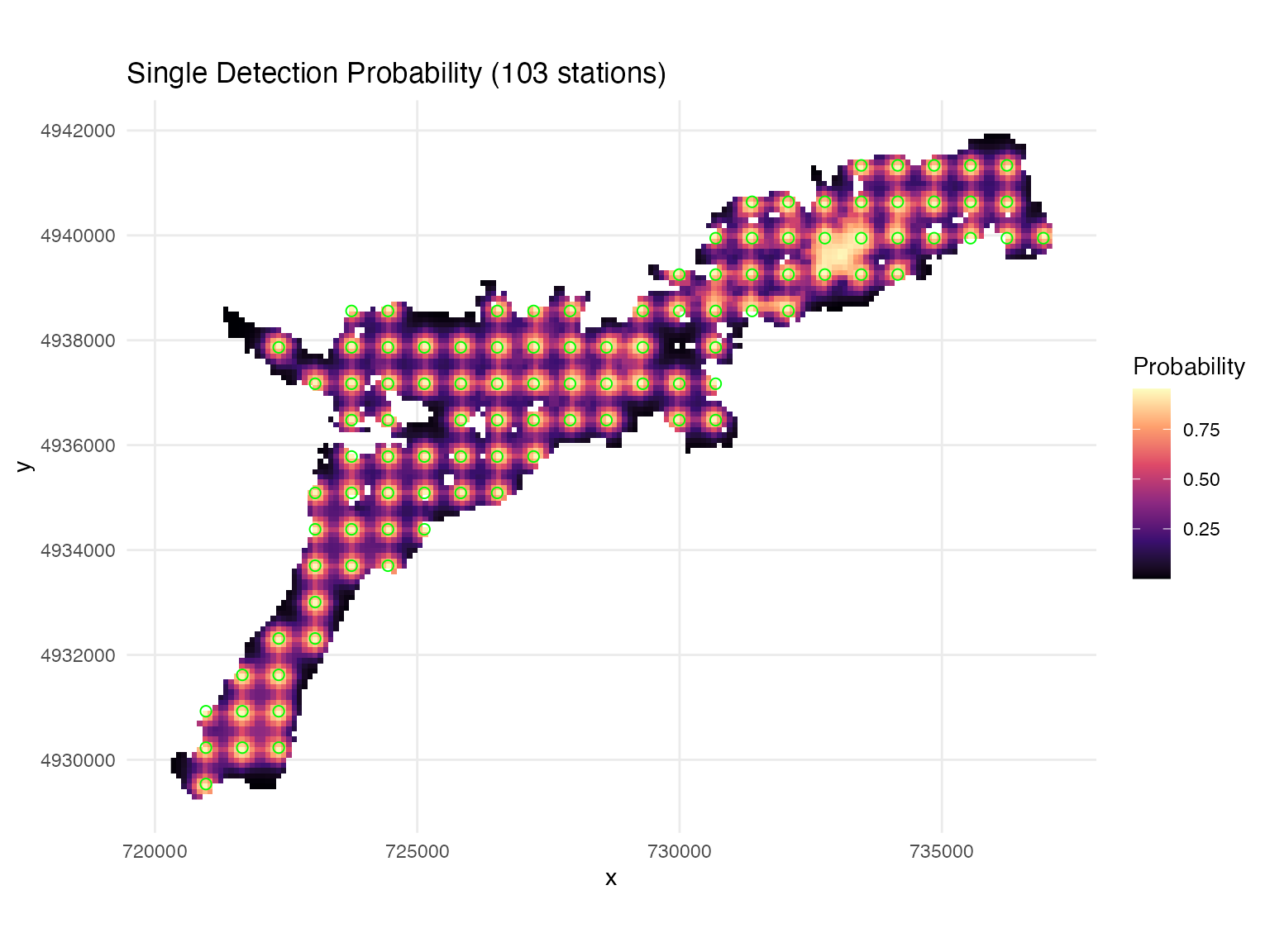
##
## === Detection System Summary ===
## Target date: All dates
## Active stations: 103
## Mean cumulative detection probability: 0.428
# Key outputs:
# system_DE$data - detection probability data
# system_DE$plots$cumulative - visualization🐟 Fish Movement Simulation
Simulating fish movements allows us to evaluate array performance under known conditions. By generating tracks with known properties, we can assess detection probability, positioning accuracy, and space use estimation methods. There are flexible options for generating simulated tracks, users are encouraged to develop movement models specific to species characteristics (see advanced simulation vignette).
Generate Realistic Fish Tracks
Generate fish movements using correlated random walks and simulate detections based on the array and detection model:
# Set start time for temporal consistency
start_time <- as.POSIXct("2025-07-15 12:00:00", tz = "UTC")
# Simulate fish tracks with detections
fish_simulation <- simulate_fish_tracks(
raster = depth_raster,
station_distances = station_distances, # Contains DE_pred values
n_paths = 10, # Number of fish
n_steps = 100, # Steps per track
step_length_mean = 50, # Average step length (m)
step_length_sd = 30, # Step length variability
time_step = 60, # Time between steps (seconds)
seed = 123,
start_time = start_time
# Optional species-specific parameters:
# species = "Walleye", # Available: "Walleye", "Smallmouth Bass", "Muskellunge"
# fish_size_cm = 45, # Fish length in cm
# behavioral_states = TRUE, # Three-state movement model
)## Preprocessing spatial lookup table...
## Generating path 1 of 10
## Generating path 2 of 10
## Generating path 3 of 10
## Generating path 4 of 10
## Generating path 5 of 10
## Generating path 6 of 10
## Generating path 7 of 10
## Generating path 8 of 10
## Generating path 9 of 10
## Generating path 10 of 10
## Simulation complete!
## Start time: 2025-07-15 12:00:00 UTC
## End time: 2025-07-15 13:40:00 UTC
# Examine simulation outputs
#head(fish_simulation$tracks) # Movement tracks
#head(fish_simulation$station_detections) # Individual receiver detections
# Visualize simulated tracks
raster_df <- as.data.frame(depth_raster, xy = TRUE)
ggplot() +
geom_raster(data = raster_df, aes(x = x, y = y, fill = layer)) +
scale_fill_gradient(low = "blue4", high = "cornflowerblue",
na.value = "transparent", name = "Depth (m)") +
geom_path(data = fish_simulation$tracks,
aes(x = x, y = y, group = path_id, color = factor(path_id)),
linewidth = 0.8) +
scale_color_discrete(name = "Fish ID") +
labs(title = "🐟 Simulated Fish Movements",
subtitle = "Correlated random walks with detection events") +
theme_minimal() +
coord_sf()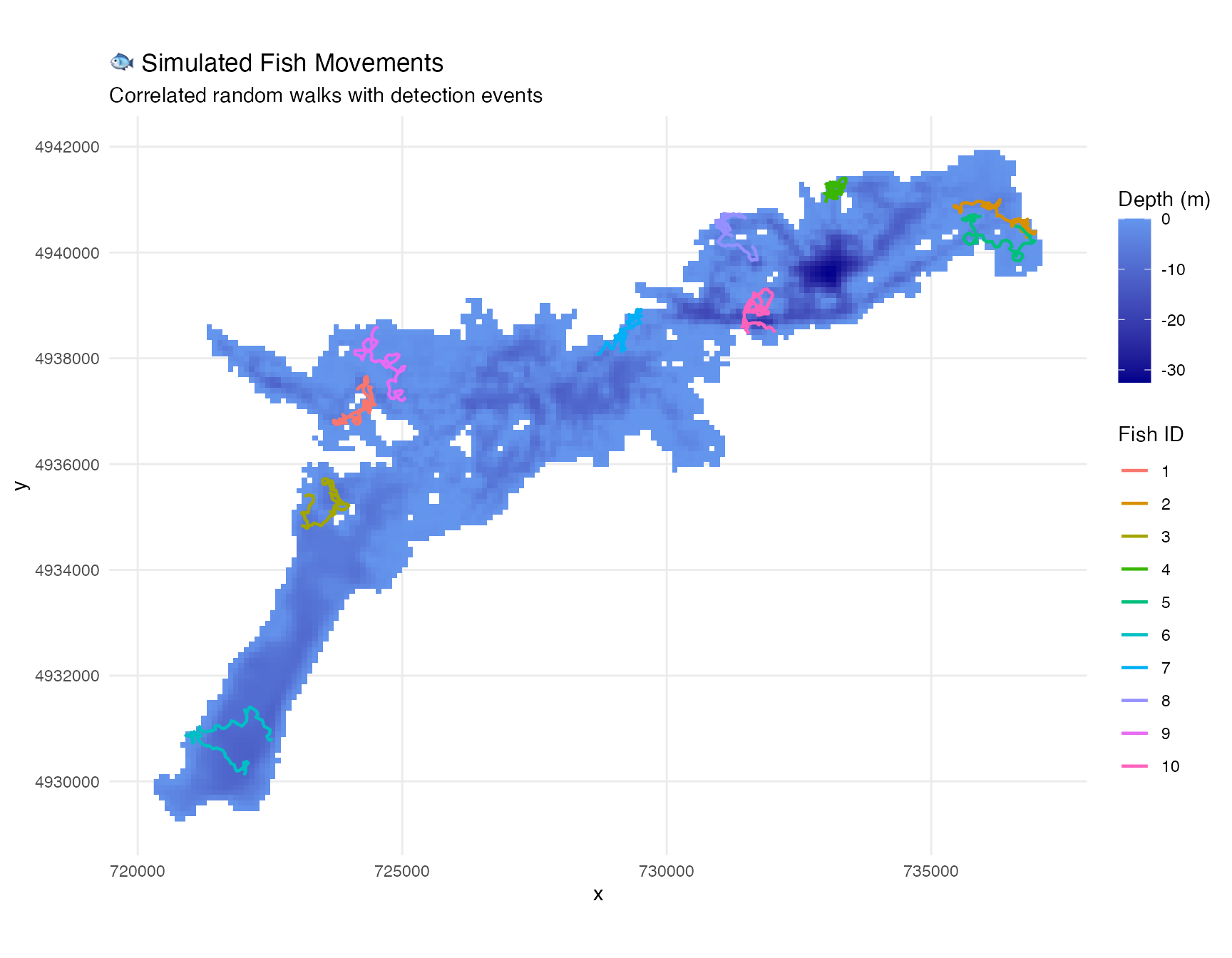
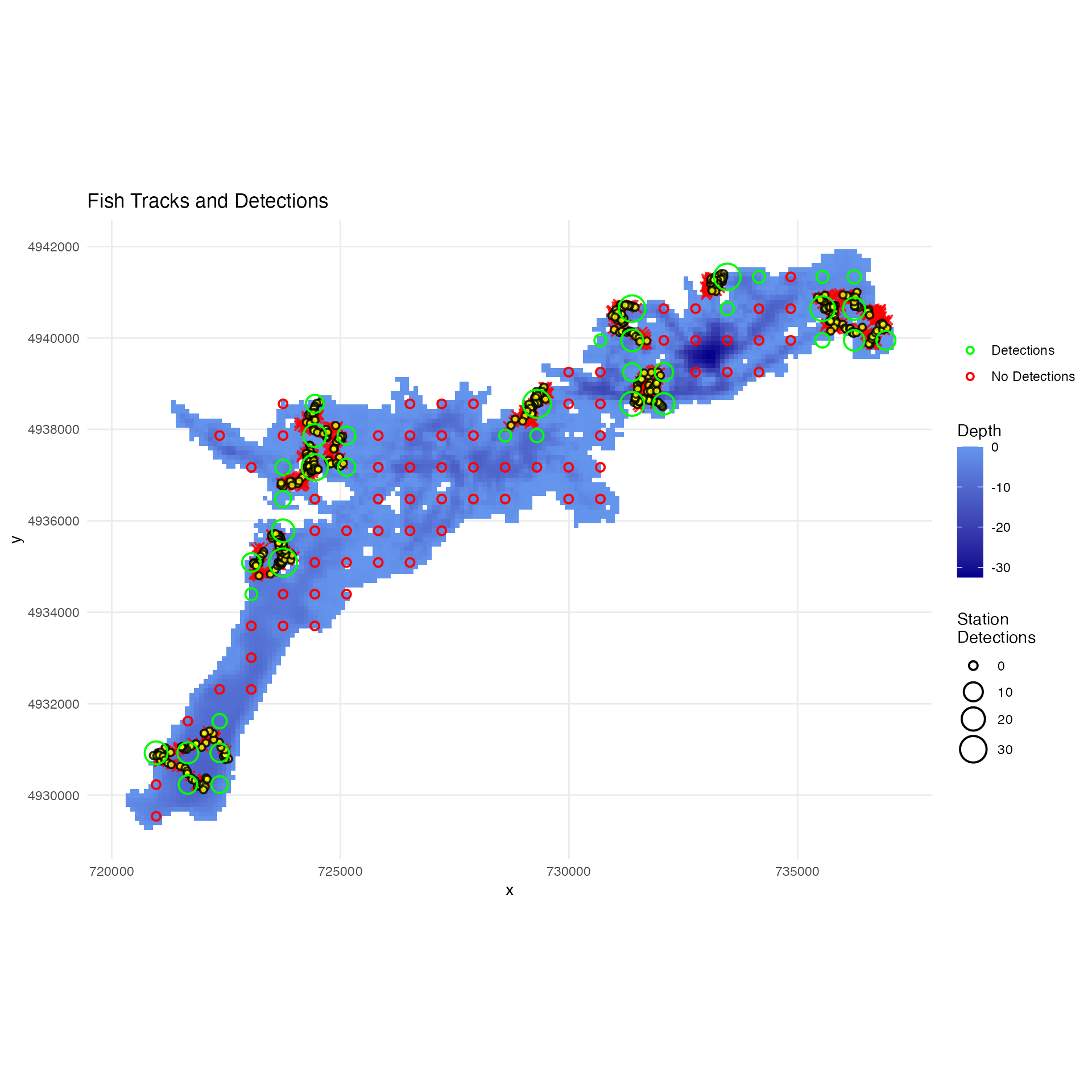
Analyze Detection Performance
Visualize tracks with detection information and analyze detection performance:
# Plot tracks with detection information
plot_fish_tracks(
fish_simulation, # Simulation outputs
depth_raster, # Depth raster
stations_regular, # Receiver array
show_detections = TRUE
)
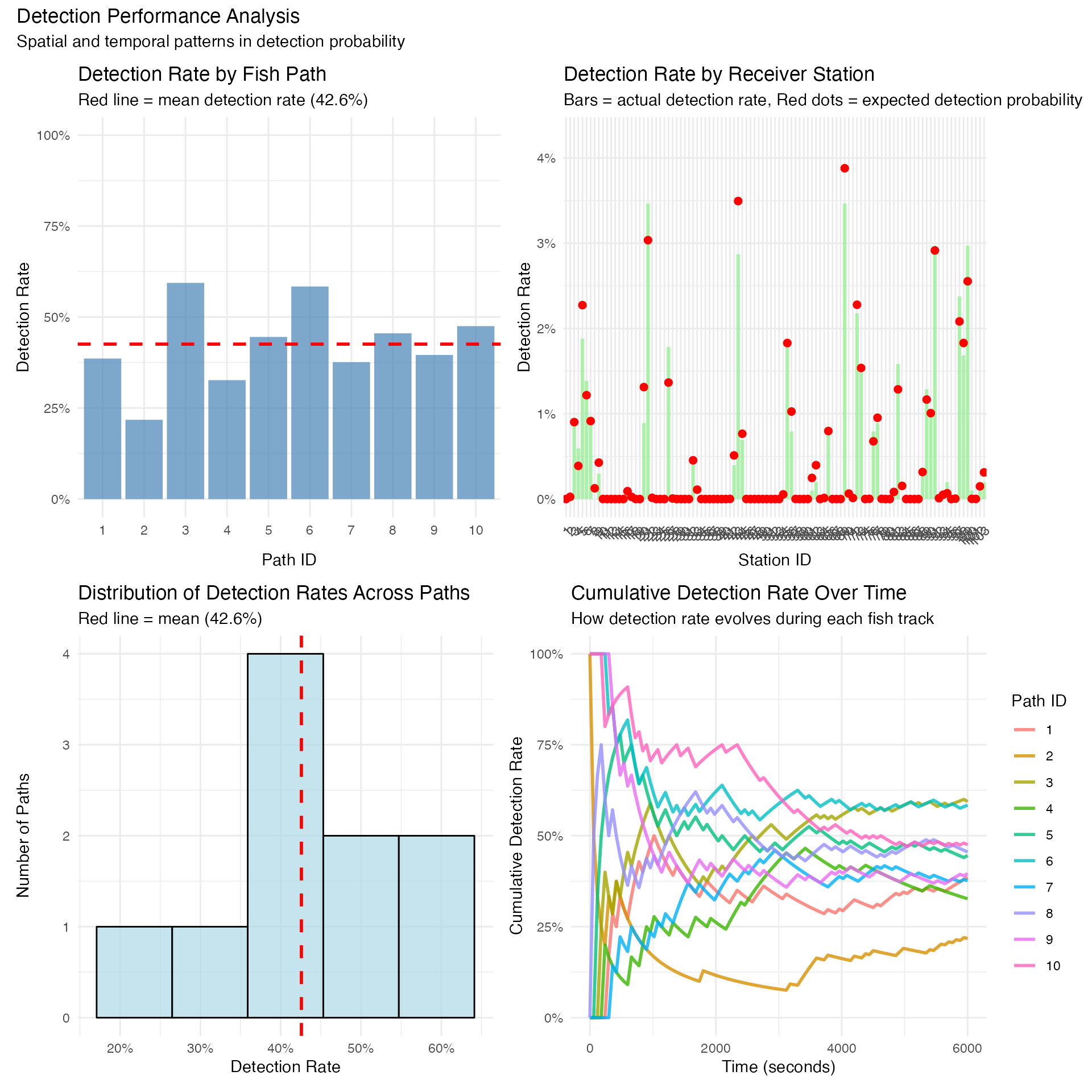
# Analyze detection performance across the array
detection_performance <- analyze_detection_performance(fish_simulation,
create_plots = TRUE,
display_plots = FALSE)## Analyzing detection performance...
##
## === DETECTION SUMMARY REPORT ===
##
## OVERALL DETECTION PERFORMANCE:
## Total steps simulated: 1010
## Steps with detections: 430
## Overall detection rate: 42.6%
##
## DETECTION RATE STATISTICS ACROSS PATHS:
## Mean detection rate: 42.6%
## Median detection rate: 42.1%
## Range: 21.8% - 59.4%
## Standard deviation: 11.3%
##
## DETECTION RATE BY INDIVIDUAL PATH:
## Path 1: 39/101 steps detected (38.6%)
## Path 2: 22/101 steps detected (21.8%)
## Path 3: 60/101 steps detected (59.4%)
## Path 4: 33/101 steps detected (32.7%)
## Path 5: 45/101 steps detected (44.6%)
## Path 6: 59/101 steps detected (58.4%)
## Path 7: 38/101 steps detected (37.6%)
## Path 8: 46/101 steps detected (45.5%)
## Path 9: 40/101 steps detected (39.6%)
## Path 10: 48/101 steps detected (47.5%)
##
## DETECTION RATE BY RECEIVER STATION:
## Station 1: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 2: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 3: 9/1010 opportunities detected (0.9%, expected 0.9%)
## Station 4: 6/1010 opportunities detected (0.6%, expected 0.4%)
## Station 5: 19/1010 opportunities detected (1.9%, expected 2.3%)
## Station 6: 14/1010 opportunities detected (1.4%, expected 1.2%)
## Station 7: 9/1010 opportunities detected (0.9%, expected 0.9%)
## Station 8: 0/1010 opportunities detected (0.0%, expected 0.1%)
## Station 9: 3/1010 opportunities detected (0.3%, expected 0.4%)
## Station 10: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 11: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 12: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 13: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 14: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 15: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 16: 1/1010 opportunities detected (0.1%, expected 0.1%)
## Station 17: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 18: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 19: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 20: 9/1010 opportunities detected (0.9%, expected 1.3%)
## Station 21: 35/1010 opportunities detected (3.5%, expected 3.0%)
## Station 22: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 23: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 24: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 25: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 26: 18/1010 opportunities detected (1.8%, expected 1.4%)
## Station 27: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 28: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 29: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 30: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 31: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 32: 5/1010 opportunities detected (0.5%, expected 0.5%)
## Station 33: 0/1010 opportunities detected (0.0%, expected 0.1%)
## Station 34: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 35: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 36: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 37: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 38: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 39: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 40: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 41: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 42: 4/1010 opportunities detected (0.4%, expected 0.5%)
## Station 43: 29/1010 opportunities detected (2.9%, expected 3.5%)
## Station 44: 7/1010 opportunities detected (0.7%, expected 0.8%)
## Station 45: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 46: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 47: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 48: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 49: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 50: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 51: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 52: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 53: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 54: 0/1010 opportunities detected (0.0%, expected 0.1%)
## Station 55: 19/1010 opportunities detected (1.9%, expected 1.8%)
## Station 56: 8/1010 opportunities detected (0.8%, expected 1.0%)
## Station 57: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 58: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 59: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 60: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 61: 1/1010 opportunities detected (0.1%, expected 0.2%)
## Station 62: 2/1010 opportunities detected (0.2%, expected 0.4%)
## Station 63: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 64: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 65: 8/1010 opportunities detected (0.8%, expected 0.8%)
## Station 66: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 67: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 68: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 69: 35/1010 opportunities detected (3.5%, expected 3.9%)
## Station 70: 0/1010 opportunities detected (0.0%, expected 0.1%)
## Station 71: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 72: 22/1010 opportunities detected (2.2%, expected 2.3%)
## Station 73: 15/1010 opportunities detected (1.5%, expected 1.5%)
## Station 74: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 75: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 76: 8/1010 opportunities detected (0.8%, expected 0.7%)
## Station 77: 9/1010 opportunities detected (0.9%, expected 1.0%)
## Station 78: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 79: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 80: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 81: 1/1010 opportunities detected (0.1%, expected 0.1%)
## Station 82: 16/1010 opportunities detected (1.6%, expected 1.3%)
## Station 83: 0/1010 opportunities detected (0.0%, expected 0.2%)
## Station 84: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 85: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 86: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 87: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 88: 3/1010 opportunities detected (0.3%, expected 0.3%)
## Station 89: 13/1010 opportunities detected (1.3%, expected 1.2%)
## Station 90: 10/1010 opportunities detected (1.0%, expected 1.0%)
## Station 91: 30/1010 opportunities detected (3.0%, expected 2.9%)
## Station 92: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 93: 0/1010 opportunities detected (0.0%, expected 0.1%)
## Station 94: 2/1010 opportunities detected (0.2%, expected 0.1%)
## Station 95: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 96: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 97: 24/1010 opportunities detected (2.4%, expected 2.1%)
## Station 98: 17/1010 opportunities detected (1.7%, expected 1.8%)
## Station 99: 30/1010 opportunities detected (3.0%, expected 2.6%)
## Station 100: 1/1010 opportunities detected (0.1%, expected 0.0%)
## Station 101: 0/1010 opportunities detected (0.0%, expected 0.0%)
## Station 102: 1/1010 opportunities detected (0.1%, expected 0.1%)
## Station 103: 2/1010 opportunities detected (0.2%, expected 0.3%)
##
## Creating visualization plots...
performance_plots <- (detection_performance$plots$by_path +
detection_performance$plots$by_station) /
(detection_performance$plots$distribution +
detection_performance$plots$time_series)
performance_plots +
plot_annotation(
title = "Detection Performance Analysis",
subtitle = "Spatial and temporal patterns in detection probability"
)
🏡 Space Use Analysis
Space use analysis is fundamental to understanding animal ecology. There are a range of options for characterizing the scale of space use (home range); constrained convex hull is most consistent with typical home range estimates, while grid cell count is more accurate to the specific locations actually occupied.
Calculate Space Use Estimates
Calculate space use estimates from the simulated tracks using multiple methods:
# Calculate space use estimates using multiple methods
space_use_results <- calculate_space_use(
track_data = fish_simulation$tracks,
by_fish = TRUE,
by_time_period = TRUE,
time_aggregation = "day", # Options: "hour", "day", "month", "none"
methods = c("convex_hull", "bounding_box", "grid_cell_count",
"ellipse_95", "constrained_convex_hull", "mcp"),
grid_resolution = 100
)
# View results
print(space_use_results$space_use_estimates)## group_id n_points range_x_m range_y_m centroid_x
## 1 fish_id=1_time_period=1752552000 101 811.4348 908.9238 724196.9
## 2 fish_id=2_time_period=1752552000 101 1544.1541 711.8670 736373.3
## 3 fish_id=3_time_period=1752552000 101 889.9452 936.6597 723553.7
## 4 fish_id=4_time_period=1752552000 101 407.9325 464.0480 733157.3
## 5 fish_id=5_time_period=1752552000 101 1370.3389 869.0523 736193.0
## 6 fish_id=6_time_period=1752552000 101 1645.5561 1282.7828 721655.1
## 7 fish_id=7_time_period=1752552000 101 880.7179 857.2038 729217.6
## 8 fish_id=8_time_period=1752552000 101 779.0324 887.4003 731201.5
## 9 fish_id=9_time_period=1752552000 101 963.6621 1393.7372 724662.5
## 10 fish_id=10_time_period=1752552000 101 633.7061 824.8583 731696.3
## centroid_y convex_hull_area_m2 convex_hull_area_hectares mcp_area_m2
## 1 4937098 370485.3 37.04853 370485.3
## 2 4940669 535166.4 53.51664 535166.4
## 3 4935255 528818.3 52.88183 528818.3
## 4 4941177 124018.2 12.40182 124018.2
## 5 4940304 746678.2 74.66782 746678.2
## 6 4930830 1166605.6 116.66056 1166605.6
## 7 4938512 301327.2 30.13272 301327.2
## 8 4940439 447067.3 44.70673 447067.3
## 9 4937873 741106.1 74.11061 741106.1
## 10 4938874 407446.2 40.74462 407446.2
## mcp_area_hectares bounding_box_area_m2 bounding_box_area_hectares
## 1 37.04853 737532.4 73.75324
## 2 53.51664 1099232.3 109.92323
## 3 52.88183 833575.8 83.35758
## 4 12.40182 189300.2 18.93002
## 5 74.66782 1190896.2 119.08962
## 6 116.66056 2110891.1 211.08911
## 7 30.13272 754954.7 75.49547
## 8 44.70673 691313.6 69.13136
## 9 74.11061 1343091.7 134.30917
## 10 40.74462 522717.8 52.27178
## grid_cells_used grid_cell_count_area_m2 grid_cell_count_area_hectares
## 1 38 380000 38
## 2 37 370000 37
## 3 37 370000 37
## 4 19 190000 19
## 5 50 500000 50
## 6 50 500000 50
## 7 32 320000 32
## 8 36 360000 36
## 9 45 450000 45
## 10 37 370000 37
## constrained_convex_hull_area_m2 constrained_convex_hull_area_hectares
## 1 390000 39
## 2 560000 56
## 3 550000 55
## 4 120000 12
## 5 750000 75
## 6 1160000 116
## 7 300000 30
## 8 430000 43
## 9 760000 76
## 10 390000 39
## fish_id time_period time_period_label
## 1 1 1752552000 2025-07-15
## 2 2 1752552000 2025-07-15
## 3 3 1752552000 2025-07-15
## 4 4 1752552000 2025-07-15
## 5 5 1752552000 2025-07-15
## 6 6 1752552000 2025-07-15
## 7 7 1752552000 2025-07-15
## 8 8 1752552000 2025-07-15
## 9 9 1752552000 2025-07-15
## 10 10 1752552000 2025-07-15
# Compare methods graphically
plot_space_use(space_use_results, plot_type = "comparison")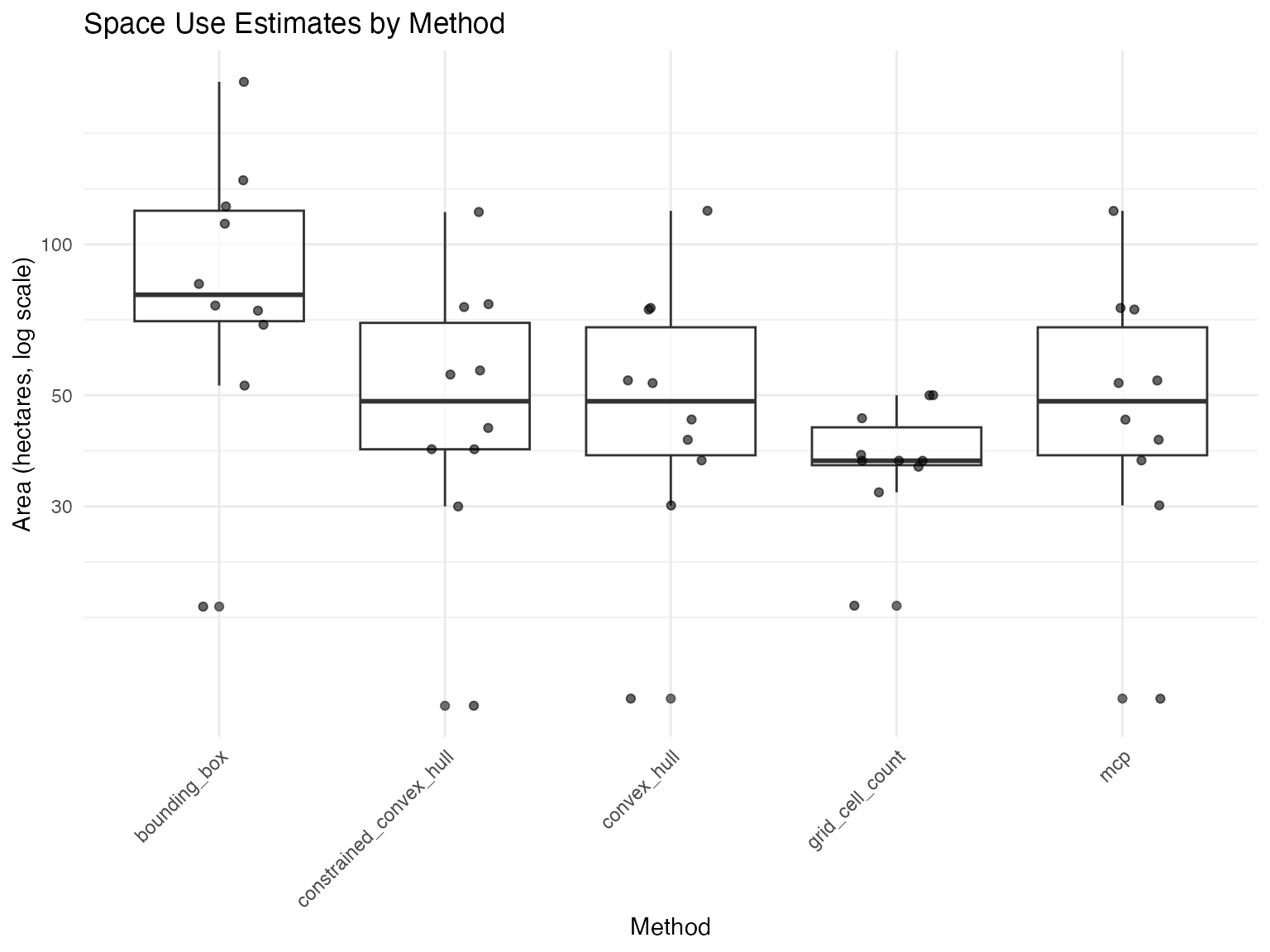
plot_space_use(space_use_results, plot_type = "by_fish")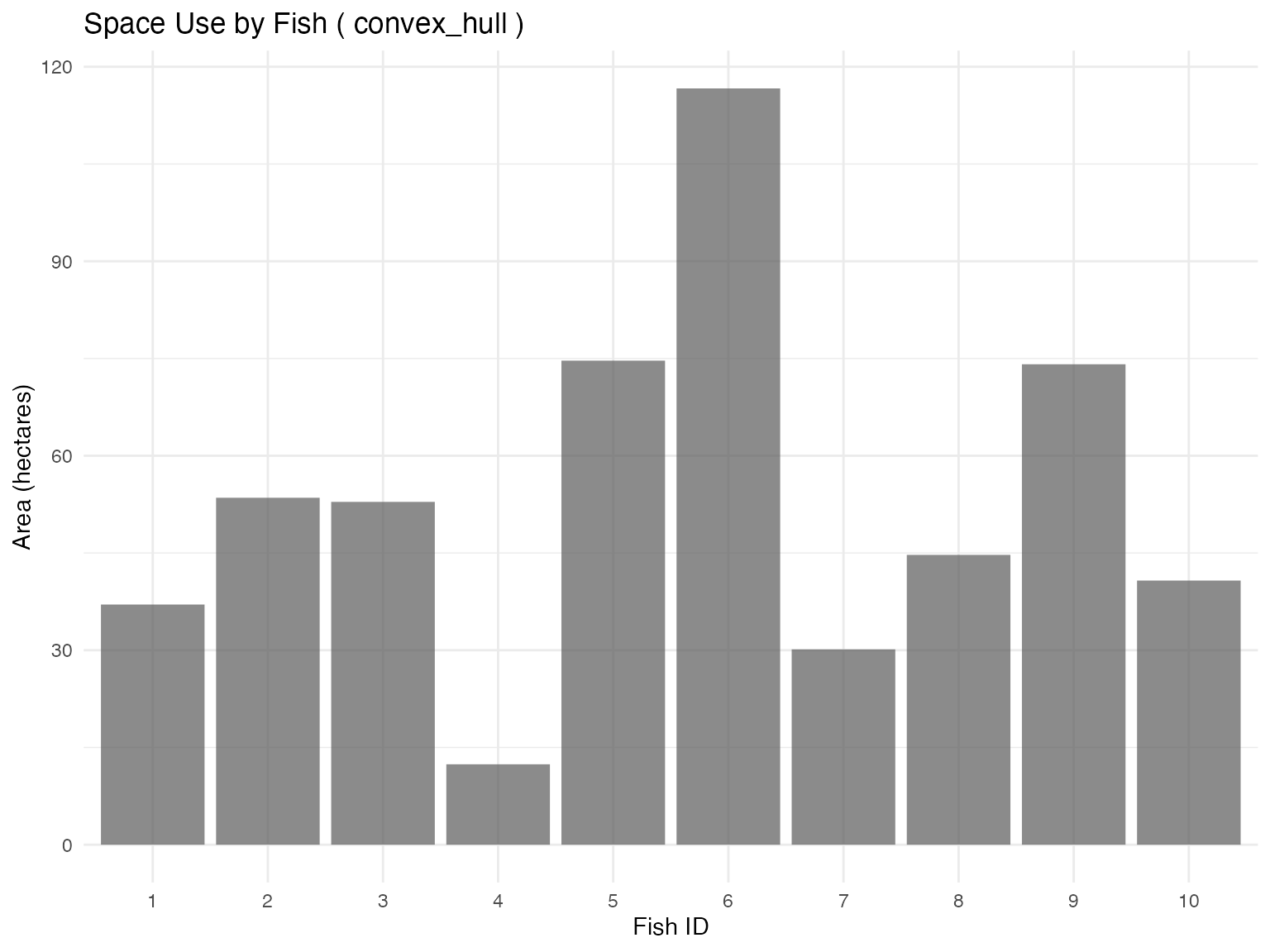
#plot outputs for select methods
# Select fish and time period
fish_select <- 1
time_select <- "2025-07-15"
# Convex hull method
plot_space_use(space_use_results,
plot_type = "map",
track_data = fish_simulation$tracks,
fish_select = fish_select,
time_select = time_select,
method_select = "convex_hull",
background_raster = depth_raster) +
ggtitle("Convex Hull Space Use")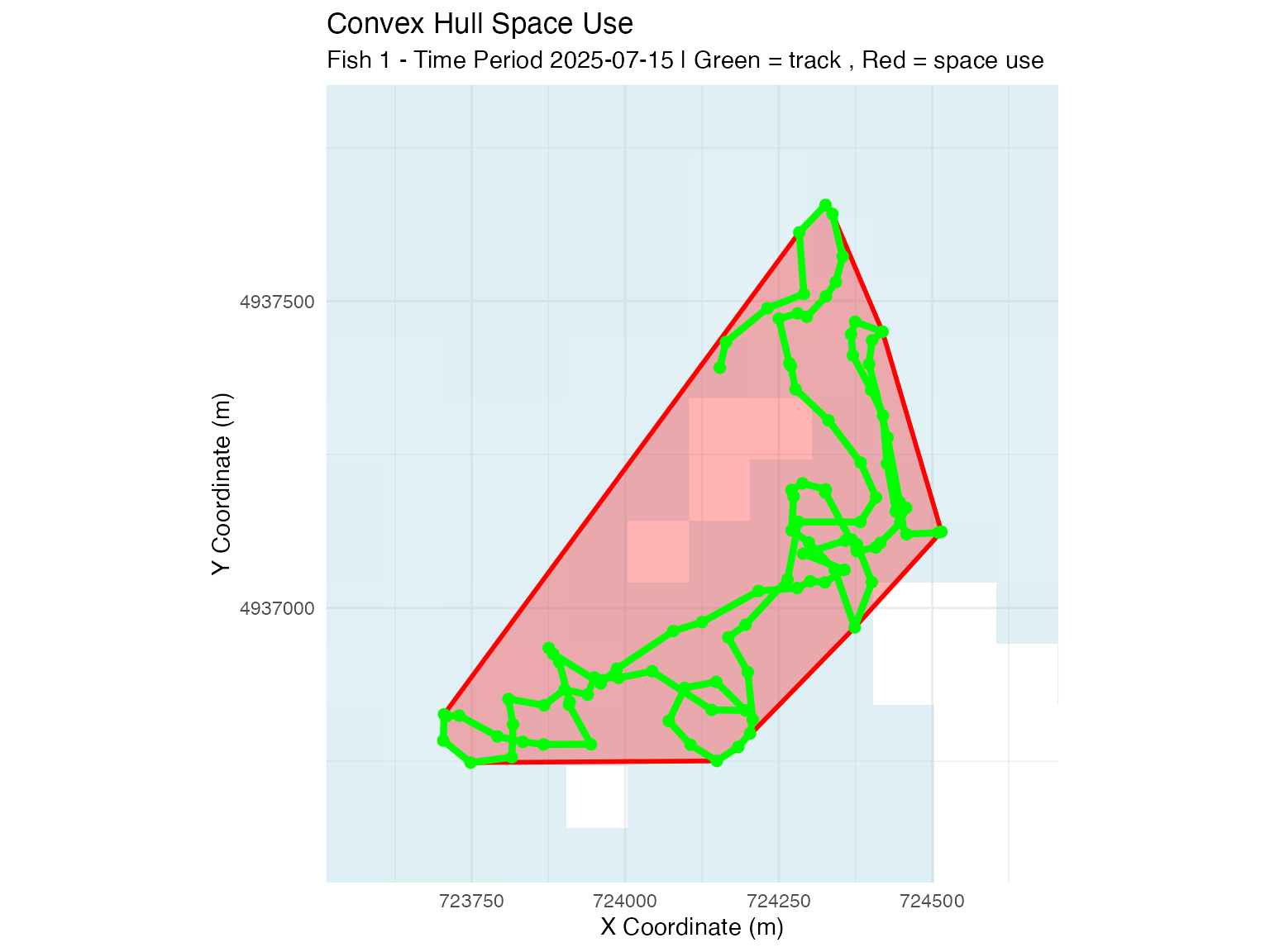
# Constrained convex hull method (raster-based)
plot_space_use(space_use_results,
plot_type = "map",
track_data = fish_simulation$tracks,
fish_select = fish_select,
time_select = time_select,
method_select = "constrained_convex_hull",
background_raster = depth_raster) +
ggtitle("Constrained Convex Hull Space Use")
# Grid cell count method
plot_space_use(space_use_results,
plot_type = "map",
track_data = fish_simulation$tracks,
fish_select = fish_select,
time_select = time_select,
method_select = "grid_cell_count",
background_raster = depth_raster) +
ggtitle("Grid Cell Count Space Use")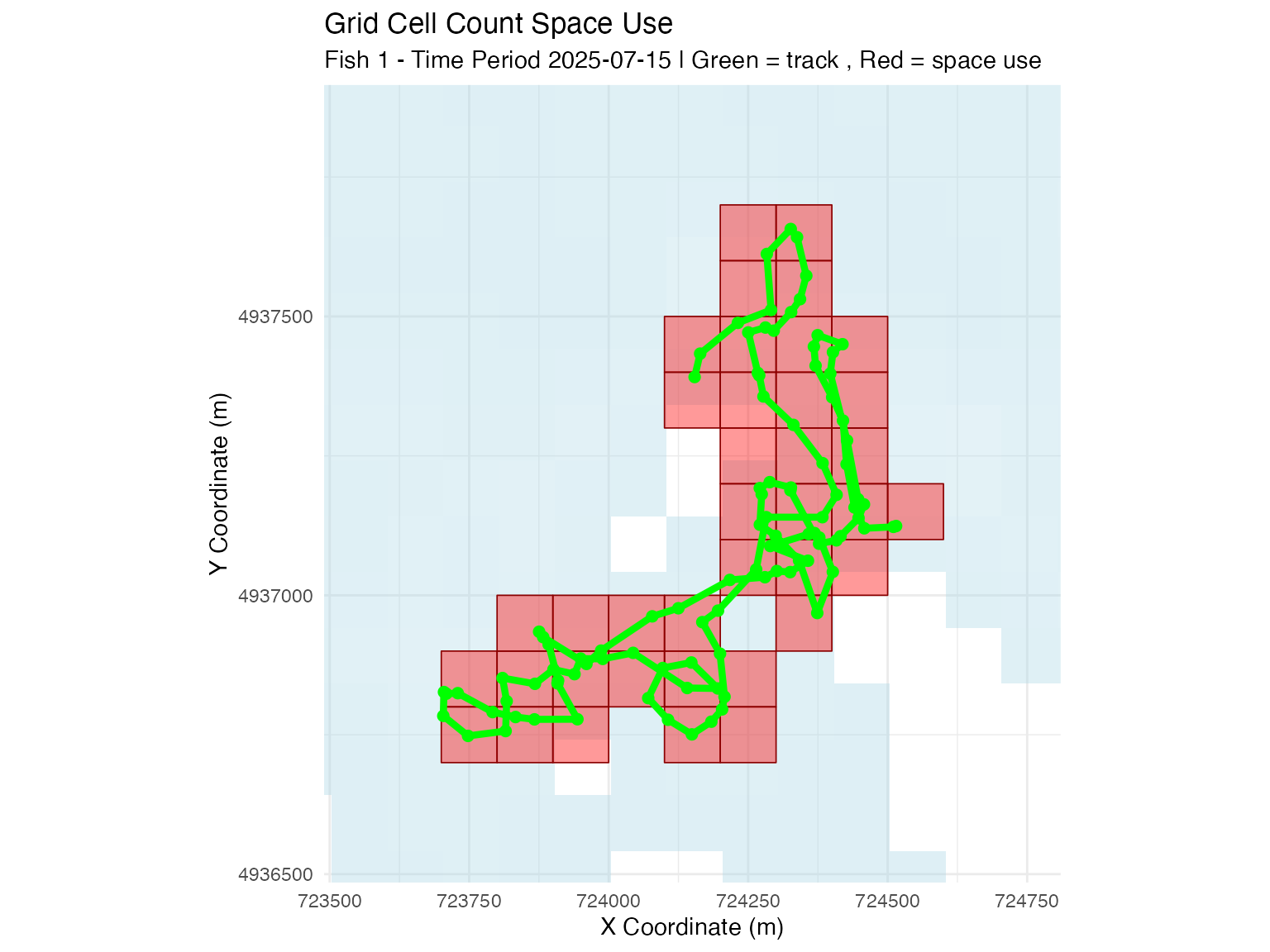
Method Selection Guide
- Grid cell count: Most representative of actual space use when tracking is consistent, but biased with detection gaps when applied to animal positioning.
- Constrained convex hull: More robust to detection gaps with animal positioning, consistent with common home range approaches
- Convex hull: Simple geometric approach, may overestimate space use in complex habitats and does not consider land.
Choose methods based on your data characteristics and research questions.
🌿 Habitat Selection Analysis
Habitat selection analysis helps identify environmental factors that influence animal distribution. By comparing used (presence) locations to available (absence) locations, we can understand habitat preferences.
Generate Presence-Absence Data
Create datasets for habitat selection analysis:
# Generate presence points within space use areas
track_presence <- sample_points_from_track_grid(
track_data = fish_simulation$tracks,
reference_raster = depth_raster,
n_points = 1000,
crs = 32617
)## === TRACK GRID SAMPLING ===
## Grid resolution: 100 meters
## Original track data: 1010 points
## Creating grid and counting track points...
## Created 360 grid cells with track points
## After count thresholds ( 1 <=count<= Inf ): 360 cells
##
## Processing 10 fish-time combinations
## fish_id = 1, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 33 cells (total usage: 101 track points)
## fish_id = 2, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 35 cells (total usage: 101 track points)
## fish_id = 3, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 37 cells (total usage: 101 track points)
## fish_id = 4, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 18 cells (total usage: 101 track points)
## fish_id = 5, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 43 cells (total usage: 101 track points)
## fish_id = 6, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 48 cells (total usage: 101 track points)
## fish_id = 7, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 29 cells (total usage: 101 track points)
## fish_id = 8, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 32 cells (total usage: 101 track points)
## fish_id = 9, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 50 cells (total usage: 101 track points)
## fish_id = 10, time_period_label = 2025-07-15, time_period_posix = 1752537600 : sampled 1000 points from 35 cells (total usage: 101 track points)
##
## === SAMPLING SUMMARY ===
## Total points sampled: 10000
## Grid resolution: 100 meters
## Fish ID(s): 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
## Time periods: 1
## Groups: 10
## Usage range: 1 to 19 track points per cell
## Mean usage: 4.68 track points per cell
# Generate absence points
track_absence<- sample_points_from_system_de(
system_DE,
position_points = track_presence,
n_points = 1000,
uniform = TRUE, #set uniform points (not relative to system DE)
min_prob_threshold = 0.1, #threshold cutoff - only points where >0.1 system DE
crs = 32617,
seed = 123
)## Using probability column: cumulative_prob
## Original data: 4818 cells
## Found 10 fish ID(s) in position_points template
## Found 1 time label(s) in position_points template
## Note: Template contains fish/time information, but system_de data lacks these columns.
## Will replicate sampling across template groups.## After probability thresholds ( 0.1 < prob < 1 ): 4331 cells
##
## Replicating sampling across template fish-time combinations
## Found 10 unique fish-time combinations in template
## fish_id = 1, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
## fish_id = 2, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
## fish_id = 3, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
## fish_id = 4, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
## fish_id = 5, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
## fish_id = 6, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
## fish_id = 7, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
## fish_id = 8, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
## fish_id = 9, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
## fish_id = 10, time_period_posix = 1752537600, time_period_label = 2025-07-15 : replicated 1000 points
##
## === SAMPLING SUMMARY ===
## Total points sampled: 10000
## Probability column: cumulative_prob
## Groups: 10
## Sampled probability range: 0.1035 to 0.951
## Mean probability: 0.4728
#plotting
ggplot() +
geom_raster(data = raster_df, aes(x = x, y = y, fill = layer)) +
scale_fill_gradient(low = "blue4", high = "cornflowerblue",
na.value = "transparent", name = "Depth (m)") +
geom_sf(data = track_presence, aes(color = count),
alpha = 0.5, size = 1) +
scale_color_viridis_c(name = "Count", option = "magma") +
coord_sf() +
theme_minimal() +
labs(title = "Track Presence Points")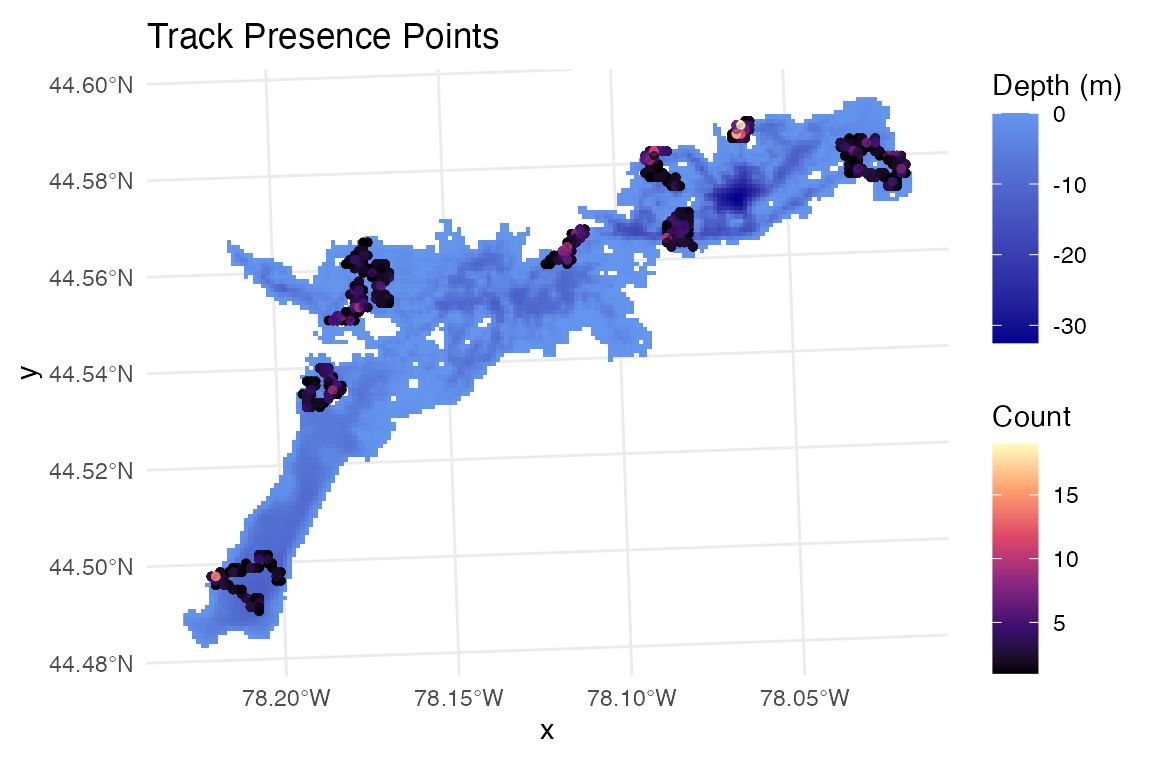
ggplot() +
geom_raster(data = raster_df, aes(x = x, y = y, fill = layer)) +
scale_fill_gradient(low = "blue4", high = "cornflowerblue",
na.value = "transparent", name = "Depth (m)") +
geom_sf(data = track_absence %>% filter(fish_id==1 & time_period_label=="2025-07-15"),
alpha = 1, size = 0.8, col="red") +
scale_color_viridis_c(name = "Cumulative\nProbability") +
theme_minimal()+labs(title="Track Absence Points (Uniform Across System)")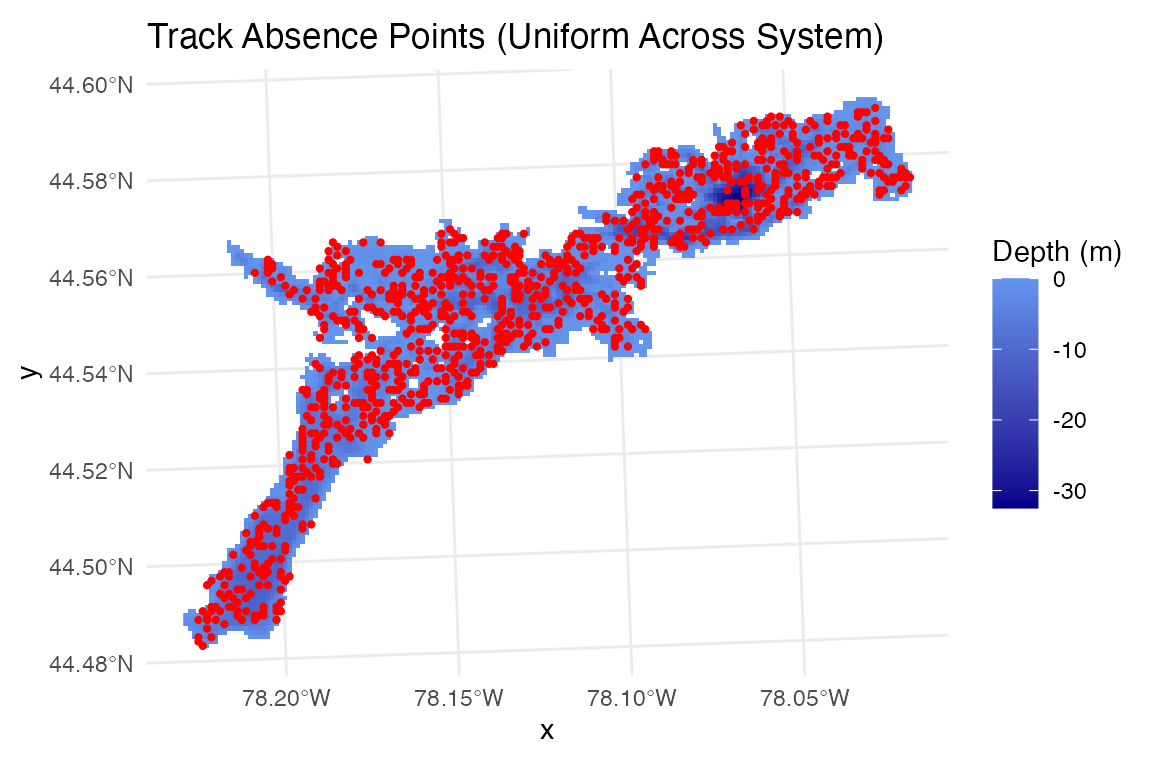
Analyze Depth Selection Patterns
# Add depth values to presence-absence points
track_presence$depth_m <- raster::extract(depth_raster, track_presence)
track_absence$depth_m <- raster::extract(depth_raster, track_absence)
# Combine presence and absence data
track_presence_absence_points <- rbind(
track_presence %>%
select(fish_id, time_period_posix, depth_m) %>%
mutate(type = "presence"),
track_absence %>%
select(fish_id, time_period_posix, depth_m) %>%
mutate(type = "absence")
)
# Analyze depth selection patterns
plot_depth_selection(track_presence_absence_points, plot_type = "density") +
ggtitle("Depth Selection from Simulated Tracks") +
labs(subtitle = "Blue = presences, Red = absences")## Plotting depth selection for 20000 points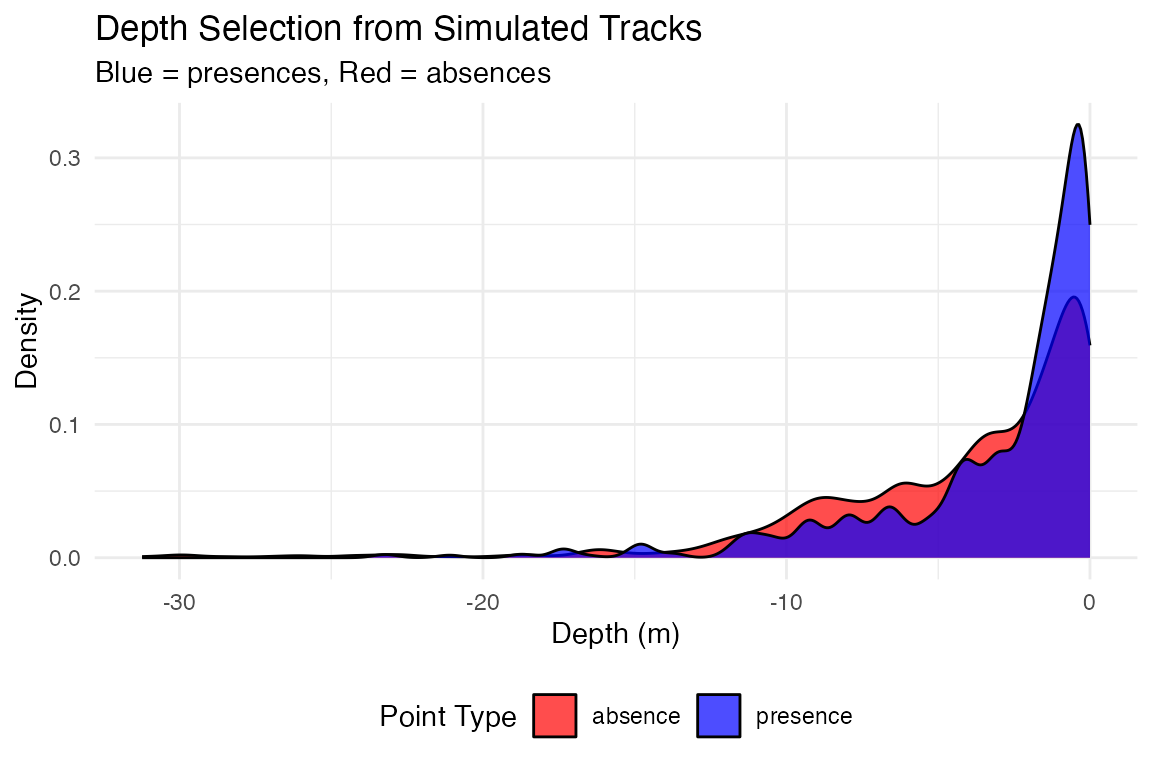
# Compare depth selection by fish
plot_depth_comparison(track_presence_absence_points,
comparison_var = "fish_id",
plot_type = "boxplot") +
ggtitle("Depth Selection by Individual Fish")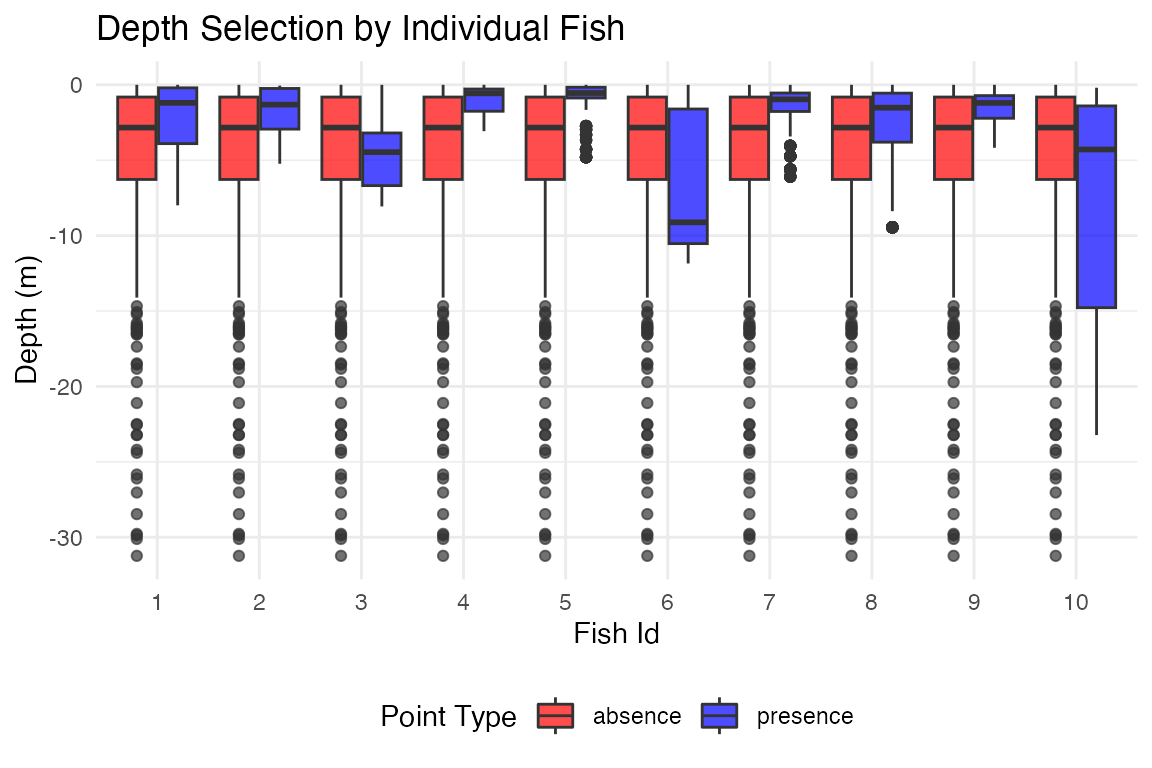
📝 Summary & Conclusions
Key Takeaways
This tutorial demonstrated a complete acoustic telemetry study workflow:
- Array Design: Generated receiver arrays with different spatial configurations
- Detection Modeling: Created depth-dependent detection range models
- Efficiency Analysis: Calculated system-level detection probabilities
- Movement Simulation: Generated realistic fish movements with detections
- Space Use Analysis: Estimated home ranges using multiple methods
- Habitat Analysis: Created presence-absence data for habitat selection studies
💡 Best Practices for Array Design
- Detection range models should be based on empirical range testing data from your study system
- Array configuration significantly affects detection probability and positioning accuracy
- System-level analysis helps identify coverage gaps and optimize receiver placement
- Simulation approaches allow testing of different array designs before costly field deployment
- Iterative refinement - use initial deployment data to improve models and optimize array expansion
- Consider environmental variability - detection ranges vary with temperature, noise, and other factors
Next Steps: - Conduct range testing in your study area to parameterize detection models - Use WADE positioning methods for fine-scale movement analysis (see WADE tutorials) - Compare multiple array configurations to find optimal design for your objectives